微积分测试卷

一、单项选择题（每题3分，共30分）

极限$\lim_{x \to \infty}(1 + \frac{1}{x})^{2x}$的值为（）
A. $e$ B. $e^2$ C. $2e$ D. $1$
若函数$f(x)=\begin{cases}x^2 + 1, & x \neq 0 \ 1, & x = 0\end{cases}$，则$\lim_{x \to 0}f(x)$等于（）
A. 0 B. 1 C. 不存在 D. 2
函数$y = \ln(x^2 - 1)$的定义域是（）
A. $(-\infty, -1) \cup (1, +\infty)$ B. $(-1, 1)$ C. $(0, +\infty)$ D. $(-\infty, 0)$
已知曲线$y = x^3 - 3x$，则其在点$(1, -2)$处的切线斜率为（）
A. 0 B. -2 C. 3 D. -3
函数$y = \sin^2 x$的导数为（）
A. $2\sin x$ B. $\sin 2x$ C. $2\cos x$ D. $\cos 2x$
设函数$y = e^{2x}$，则$dy$等于（）
A. $e^{2x}dx$ B. $2e^{2x}dx$ C. $2e^{2x}$ D. $e^{2x}$
不定积分$\int \frac{1}{\sqrt{1 - x^2}}dx$等于（）
A. $\arcsin x + C$ B. $-\arccos x + C$ C. $\arctan x + C$ D. $-\arccot x + C$
定积分$\int_{1}^{e}\frac{1}{x}dx$的值为（）
A. 0 B. 1 C. $e$ D. $e - 1$
下列微分方程中，是一阶线性微分方程的是（）
A. $y’ + y^2 = x$ B. $y’ + xy = \sin x$ C. $y’’ + y = 0$ D. $(y’)^2 + y = e^x$
函数$z = xy$在点$(2, 3)$处的全微分$dz$为（）
A. $2dx + 3dy$ B. $3dx + 2dy$ C. $6dx + 6dy$ D. $5dx + 5dy$

二、填空题（每题3分，共15分）

极限$\lim_{x \to 0} \frac{\tan 2x}{3x} =$______。
函数$y = e^x - x$的极小值点为______。
定积分$\int_{0}^{\frac{\pi}{2}}\cos xdx =$______。
已知函数$z = \ln(x + y)$，则$\frac{\partial z}{\partial x} =$______。
二重积分$\iint_{D}(x + y)d\sigma$（其中$D$为矩形区域：$0\leq x\leq 1$，$0\leq y\leq 2$）的值为______。

三、解答题（共55分）

（5分）求极限$\lim_{x \to 0} \frac{(1 + x)^5 - 1}{x}$。
（10分）求函数$y = \frac{x^3}{3} - x^2 + 2$的凹凸区间和拐点。
（10分）计算不定积分$\int x e^x dx$。
（10分）计算定积分$\int_{-1}^{1}(x^2 + 1)dx$。
（10分）求微分方程$xy’ - y = x^2\ln x$的通解。
（10分）设函数$z = f(x, y) = x^3y^2$，求$\frac{\partial^2 z}{\partial x^2}$，$\frac{\partial^2 z}{\partial y^2}$，$\frac{\partial^2 z}{\partial x\partial y}$在点$(1, 2)$处的值。

参考答案

一、单项选择题

B 2. B 3. A 4. A 5. B 6. B 7. A 8. B 9. B 10. B
二、填空题
$\frac{2}{3}$ 2. $x = 0$ 3. 1 4. $\frac{1}{x + y}$ 5. 3
三、解答题
解：利用等价无穷小替换，当$x \to 0$时，$(1 + x)^5 - 1\sim 5x$，则原式$=\lim_{x \to 0} \frac{5x}{x}=5$。
解：
- 先求一阶导数$y’ = x^2 - 2x$，再求二阶导数$y’’ = 2x - 2$。
- 令$y’’ = 0$，解得$x = 1$。
- 当$x \lt 1$时，$y’’ \lt 0$，函数为凸函数，凸区间为$(-\infty, 1)$；当$x \gt 1$时，$y’’ \gt 0$，函数为凹函数，凹区间为$(1, +\infty)$。
- 拐点为$(1,\frac{4}{3})$。
解：利用分部积分法，设$u = x$，$dv = e^x dx$，则$du = dx$，$v = e^x$，原式$=x e^x - \int e^x dx = x e^x - e^x + C$。
解：$\int_{-1}^{1}(x^2 + 1)dx = (\frac{1}{3}x^3 + x)\big|_{-1}^{1}=(\frac{1}{3}+1)-(-\frac{1}{3}-1)=\frac{8}{3}$。
解：
- 原方程变形为$y’ - \frac{y}{x} = x\ln x$，这是一阶线性微分方程。
- 先求对应的齐次方程$y’ - \frac{y}{x} = 0$的通解，其通解为$y = Cx$。
- 设原方程的特解为$y^* = x(Ax + B)\ln x$，代入原方程可得$A=\frac{1}{2}$，$B = 0$，特解为$y^*=\frac{1}{2}x^2\ln x$。
- 所以原方程通解为$y = Cx+\frac{1}{2}x^2\ln x$。
解：
- 先求$\frac{\partial z}{\partial x}=3x^2y^2$，则$\frac{\partial^2 z}{\partial x^2}=6xy^2$，在点$(1, 2)$处，$\frac{\partial^2 z}{\partial x^2}\big|_{(1,2)}=6\times1\times2^2 = 24$。
- 再求$\frac{\partial z}{\partial y}=2x^3y$，则$\frac{\partial^2 z}{\partial y^2}=2x^3$，在点$(1, 2)$处，$\frac{\partial^2 z}{\partial y^2}\big|_{(1,2)}=2\times1^3 = 2$。
- 又$\frac{\partial^2 z}{\partial x\partial y}=6x^2y$，在点$(1, 2)$处，$\frac{\partial^2 z}{\partial x\partial y}\big|_{(1,2)}=6\times1^2\times2 = 12$。

封面作品P站id：98968620

常用网址类：

Bilibili a冥灵吧

不知道

空

过wyy下载ncm屏蔽，直接下载后打开可用
链接：https://pan.baidu.com/s/1rmK9KxfjXQsdj0yqMpjNEA
提取码：clzu
复制这段内容后打开百度网盘手机App，操作更方便哦

下面是给另一个网站提供的md。和本网站无任何关系！如果您跟着下边的操作发生了任何损失，本人不负责！！！！！！！！！！！！！

获取您的cookie(曲奇饼🍪)操作指引

Cookie是什么？

Cookie，有时也用其复数形式 Cookies。类型为“小型文本文件”，是某些网站为了辨别用户身份，进行Session跟踪而储存在用户本地终端上的数据（通常经过加密），由用户客户端计算机暂时或永久保存的信息。

我如何获取我的Cookie？

只需要简单几步，您就可以获得您的cookie：

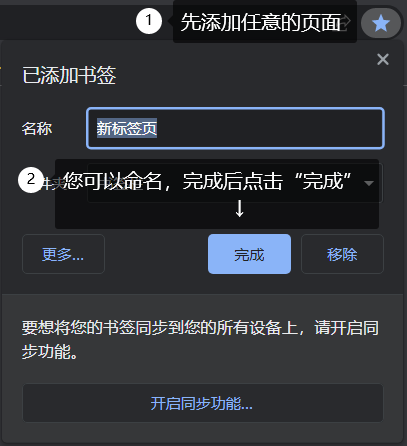
1.前往您的书签，任意保存一个页面，如下图所示

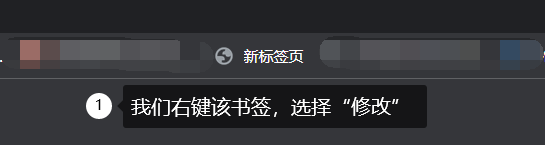
2.右键该书签，找到“修改”选项，打开该窗口
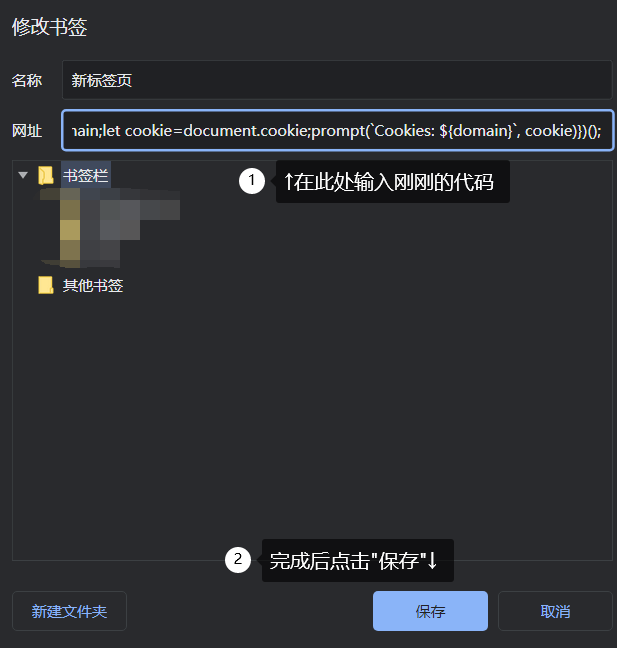
3.将下列代码复制进入“网址”输入框处，并完成关闭
1
2
3
4
5
6
7
javascript:(
   function () {
       let domain=document.domain;
       let cookie=document.cookie;
       prompt(`Cookies: ${domain}`, cookie)
       }
)();